The trace of ammonia proved challenging to fit. It was modeled as a function of glutamate and the number of cells in the broth. Ammonia concentration was higher towards the middle of the batch but as glutamate became zero, it started to decrease.

The results of the final model fitting are depicted in Figure 17. The incorporation of cell death, kd, shows up by the end of the process (around day thirteen) where the predicted cell count data starts to decline. Glucose consumption from day zero was captured well until day three. The model included the fed-batch glucose strategy as part of the nutrient feed. Hence, we see an increase in glucose concentration around day one and day two. Around day three, a Raman-based glucose feedback loop was activated (Matthews, Smelko et al. 2018). The model includes a feedback controller tuned to respond to the glucose consumption rate of the cells. Lactate concentration was captured as well and included two rate expressions (lactate production and lactate consumption) attributed to the Warburg effect. Glutamine consumption rate was captured for the first two days until the initial glutamine (found in the basal media) was consumed.

To further assess the agreements between model fi t and actual process data, we made some comparison plots of the predicted versus actual data. The correlation coefficient (R2) and Root Mean Square of Estimation (RSME) between the model and actual data is shown in Figure 18. Glucose had a R2 of 97% with a RSME 0.7 g/L and the cellular growth is modeled at 92% with a RSME of 1.8 x 106 vc cells/mL. As previously discussed, ammonia and glutamine were not fitted well with our model with R2 of 25% and 30% respectively. However for titer, pH, Osmo, Lac, and DO the R2 between the model predicted and the actual data were above 80%. Thus, the model was able to capture the major dynamics of the process from day zero until harvest at day fourteen. This model was compared to other batches not used to fi t the model and showed similar results.

American Pharmaceutical Review is the leading review of business and technology for the pharmaceutical industry throughout North America. A Publication of See our other sites »

Dr. Romero-Torres is a Senior Manager of Advanced Data Analytics at Biogen where she leads a team of mathematicians, statisticians and Advanced Process Control engineers. She has over 15 years of experience in the fielding of Process Analytical Technologies (PAT) and advanced manufacturing of bio-pharmaceuticals with a focus in the use of advanced sensors, advanced process control, data analytics, machine learning and operational excellence tools. She obtained a doctorate in pharmaceutical PAT from Purdue University in 2006 and has worked for companies such as Schering Plough, Wyeth, and Pfizer. In 2014, Dr. Romero-Torres founded Bio-Hyperplane LLC, a data analytics and consultation company. At Bio-Hyperplane LLC, Romero-Torres worked with a broad portfolio of industries including biopharma, automation software (semiconductors), data analytics software and instruments. Her personal mission is advancing pharmaceutical manufacturing processes to enhance plant operations and, more importantly, improving patients’ access to critical therapies.

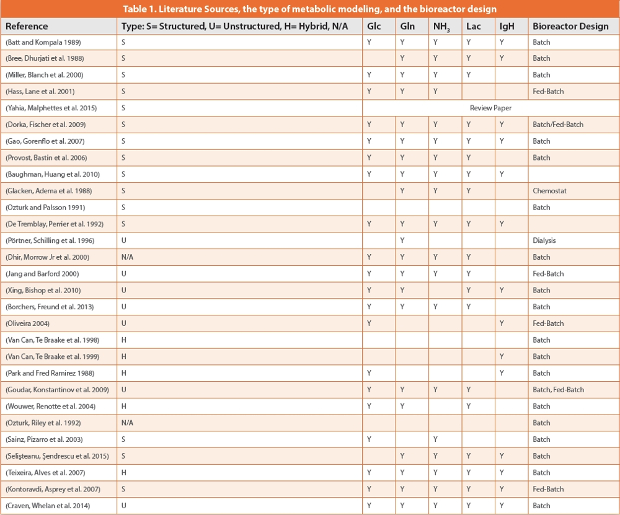
When surveying related scientific literature, it is evident that modeling scientists have gravitated towards structured models adding complexity and incorporating multiple components of the broth. See the graph in Figure 7 for a summary of the literature review and Table 1 in the Appendix for the literature source for this graph. Most of the models in literature declare constant temperature and dissolved oxygen assuming strict control for these two variables while mass balances are done on glucose, glutamine, ammonia, and lactate. Some modelers in the literature survey also add the produced titer to the overall mass balance whereas proline comes out as an important amino acid as some Chinese Hamster Ovary (CHO) cells cannot produce it. Some articles have looked at simplified metabolic pathways to track the production of the cells and consumption of nutrients (Dorka 2009).

Pre-feeding glutamate data was captured daily in the bioreactor. Even though the glutamate feeds were not measured, the model included glutamate feeding effects. The model also includes the production of glutamate by glutamine as part of the metabolism of the cell in the initial stage of the production stage.

It is advisable that models used to optimize complex processes are either based on fi rst principles, or at least hybrids (i.e. combination between empirical and first principles). Scientifically sound models are critical to ensure control strategy robustness. Generating hybrid models is not trivial as a certain degree of fundamental relationships needs to be translated to mathematical terms and combined with empirical relationships. This paper presents our team efforts to construct a hybrid model to simulate a high titer production bioreactor.

The production bioreactor process is a key step during the production of monoclonal antibodies (mAbs). This step is also known as the “N” step. The steps before the production bioreactor are commonly referred to as N-1, N-2, and so on depending on the configuration of the previous steps (seed train). The production bioreactor is the longest process during the mAbs production and requires a significant amount of nutrients and controls. Capturing the growth of cells in a fed-batch bioreactor through fundamental relationships can help us better understand the process and develop advanced process controls that can optimize feeds and maximize production. The bioreactor ecosystem can be split into four sub-systems that interact with each other: 1. Biological System 2. Solution Chemistry 3. Process Control Systems 4. Design System (see schematic of sub-systems in Figure 5). During this work, we will address three of the four sub-systems assuming no design differences in our 15,000 L bioreactor. The biological system includes all the metabolic reactions and interactions with the automation control system. The solution chemistry (the composition of the culture broth) impacts the growth of the cells and the quality of the product. The automated control strategy of a bioreactor is responsible for maintaining adequate temperature, pH, dissolved oxygen (DO), and nutrient levels. The modeled production bioreactor has seven control loops to keep the process under a state of control. The solution chemistry impacts the environment that the cells experience (osmolality, pH etc.) and other factors that directly affect the biological system. The design of the bioreactor includes hydrodynamics and other systems of the design of the bioreactor.

Used medivator · MEDIVATORS - SSD - 102LT Processor · Trusted Seller · Medivators ECA-100G · Medivators DSD-1087 · Medivators TP1 Transfer Pump · Medivators ...

PartSource - Whitby - phone number, website, address & opening hours - ON - New Auto Parts & Supplies.

The final model of the bioreactor includes the cell growth, glucose consumption, lactate, glutamine, glutamate, ammonia and titer. As mentioned above, we did not model the hydrodynamics of the bioreactor design. In this model metabolites and associated metabolic pathways (Figure 16), were simplified. This model can be augmented to include more metabolic pathways for the specific CHO cell line that produces this mAb by including targeted experiments. However, during this evaluation we just wanted to capture the major pathways using readily available measurements. The full model equation set is described in Equation 5. This model also included a parameter to account for cell death, kd. In addition, the conversion of glutamine (Gln) to glutamate (Glu) was captured in a mass balance as well as the production of ammonia (NH3). Osmolality, pH, and dissolved oxygen equations are also incorporated in the model. Osmolality and pH were fitted with a simple fitting parameter that was adjusted as different events in the process started or ended (examples are glucose feeding and cell growth stages). These parameters were fitted with the global search algorithm discussed above. The results of the entire simulation are shown in Figure 17. Even though the data does not show the glutamate amount post feeding due to the sampling strategy, the glutamate feeding was captured. In addition, the effect of this feed on osmolality was captured in the model.

... Purple · Red · Pink · White · Black · Brands · Window covering · Interior advice · Contact ... Farrow & Ball wallpaper Auguste - 6505. Article code 6505. This ...

Data was conditioned by removing outliers and measurement artifacts. After the data and equations were prepared, the next step during parameter fitting was to chose an optimizer that gives a global solution. In Figure 12 an example is given of a global search for the minimum. The global minimum is pointed out among other minima. If the solver is not able to explore outside the valley, it may never find the global mimimum. Matlab’s Global Optimization Toolbox (Version 3.4.4) has a number of algorithms such as genetic algorithm, pattern search and particle swarm (among others) (Chipperfield, 1995). The Matlab script was written to find the best fit. The Matlab script ran a local optimizer first (named fmin) by an initial guess and compared it to the output of three global optimization algorithms (namely genetic algorithm, pattern search and particle swarm). The initial set of parameters fed to the three global optimization algorithms were chosen arbitrarily. The output of the three global search algorithms was sent to the local optimizer (fmin) to improve the local solution. This resulted in four sets of solutions. The solution that gave the minimum Root Mean Square Error (RSME) allowed us to obtain the optimal parameter set. In addition, a visual check was done to rule out any solutions that didn’t meet the criteria for an adequate simulation.

The next evolution of the model included variables such as Glutamate (Glu), Glutamine (Gln), Ammonia and Titer. In addition, the glucose feedback control loop shown in Figure 6 was incorporated into the model. The loops in red are integrated in the model. Figure 14 shows a block diagram of the controllers’ inputs/outputs and how they should interact with the hybrid model of the bioreactor.

Our first bioreactor model only described the glucose to lactate reaction in a batch configuration. At this modeling stage, we ignored the other metabolites and fitted the parameters to the model’s Ordinary Differential Equations (ODE). In the set of ODEs depicted in Equation 1, the X represents the biomass, the S represents the substrate (glucose in this case), Lac represents Lactate, Ks is the Monod constant, and Yi are yields. Matlab 2018 was used to fit actual process data to these fundamental relationships by using a genetic model fitting algorithm. Figure 9 depicts the data used for this modeling step. This data was obtained from a small-scale experiment during which the cells were allowed to die of nutrient starvation after an initial feeding. Figure 10 shows how this over-simplistic model captured glucose consumption and cell growth but did not capture cell death nor lactate consumption. Equation 1 assumes only lactate accumulation and no lactate consumption. Lactate lack-of fit was addressed through fed-batch configuration modeling (discussed in the next section).

Feedback loops are implemented in a simple gain control (or proportional controller) where the error from setpoint determines the control move. For example, for glucose control, the number of grams of glucose to feed can be represented as FGlc = Kc (eGlc). Here, new flowrate request of glucose, FGlc, is equal to a proportional constant, Kc, and the error between the glucose measurement and the glucose setpoint, eGlc. Proportional controllers work well under normal operating conditions but face issues in the presence of disturbances given that they cannot maintain low errors and an offset can occur. For this reason, a proportional-integral (PI) controller (like the one shown in Equation 4) is a more appropriate strategy to control a process. The integral part of the controller includes an integral time constant, T, which changes the flow based on the error and how much time it has persisted. This strategy was implemented into the model equations and the optimizer. The control tunings were also optimized to match the available data set. Figure 15 shows the effect of the PI controller with the glucose setpoint at 3.3 g/L. The glucose trend outputed by the model is now closer to the actual manufacturing data.

QTY. 1. MOTOR: DAYTON MODEL 1D093 NO: 7121-9125 E47479 E37403 LR36496 TYPE: U21B CLASS B AMB 40... Click to Request Price. WDM B ...

Classic automation control strategies use regulatory controls to maintain process variables at predefined set-points (Al-Rubeai 2015). Regulatory loops such as proportional, proportional-integral, and proportional-integral-derivative, are used to enable feedback control strategies. These control strategies aim to control the process outcome by controlling the process set-points to predefined values and within pre-defined ranges. The pre-defined set-points are locked down under the assumption that they are a global optimal or very close to a global optimal (within equipment constraints). Nevertheless, other sources of variability (such as human intervention, equipment drift, environmental fluctuations and raw material variability) could disturb the manufacturing process leading to deviations from optimal state/conditions. In these cases, it is desirable to re-calculate, in real-time, new optimal conditions to increase, or decrease, a particular process output based on the new disturbed process state. Based on the new conditions, new set-points can be directed to the controller to ensure output optimality within the new state. Control strategies that recalculate new optimal set points based on the process condition use process models at their core and are part of the Advanced Process Control (APC) toolbox.

Rob has worked in multiple capacities in the chemical and pharmaceutical industries for more than 20 years. Rob currently leads the Global Process Analytics Center of Excellence since joining Biogen in 2015. The mission of the group is to deliver analytical capabilities for monitoring and controlling manufacturing processes. Capabilities the team supports include data systems, process condition monitoring, continued process verification, advanced process control, machine learning approaches, process modeling, knowledge management and process analytical technologies. He is currently leading efforts towards Industry 4.0 and Business Process Management. Prior to his current role, Rob spent 12 years at Merck (MSD) in various leadership capacities working on PAT, strategic initiatives and knowledge management. Rob started his career and spent 7 years at the Dow Chemical Company in the Central R&D division working in process analytics and molecular spectroscopy. Rob received a B.S. in Chemistry from the University of Massachusetts - Lowell and a Ph.D. in Analytical Chemistry from the University of Florida. Rob is a certified Inclusion Strategy Partner (KJGC), Transformational Change Agent (Conner Methodology) and Lean Six Sigma Black Belt (DFSS, DMAIC) who has numerous publications and invited presentations on Manufacturing Intelligence, PAT, Quality by Design, Strategy, Inclusion and Knowledge Management. He is very engaged in external industry activities serving on the Pharmaceutical Process Analytics Roundtable committee and the BPOG Technology Roadmap steering committee.

Bioprocess models can range from simple unstructured non-segregated to structured segregated models (Birol, 2002 ). In unstructured non-segregated models, the cell population is treated as a single component (i.e. homogenous biomass). Unstructured non-segregated models are simple approaches and applicable to many situations. Monod kinetics (Monod 1949) are an example of unstructured, nonsegregated models. In structured segregated models, cell populations are treated as a multicomponent system of cellular subcomponents and cofactors.

MD-0301 BT.

In order to start the optimization process, we selected the sum of squared error between the data and model as the objective function. We constrained the μmax as well as yield constants, Yi, and the Monod constant, Ks. See the summary in Equation 3.

In Equation 2, X represents cells, S represents glucose, V is volume, μ is growth rate, and F is the Feed of nutrients and glucose. In these ODE equations, we also added a maintenance term namely mx. This maintenance term allows for other operations that happen in the cell to be lumped together in a single empirical model parameter. As described in the previous section, for the small scale process the actual lactate content increases in the beginning of the run and then decreases. This lactate trajectory is also observed when using the fed-bach configuration at the production scale, although with different lactate production rates and at diff rent times. We modeled this lactate trajectory in a piecewise function. It was modeled in this unique way because we wanted to capture the Warburg effect (Hefzi, 2018). The Warburg effect is observed in a culture when the rate of glycolysis increases, resulting in higher lactate concentration. Parameters such as the yield constants, Yi, the maintenance term, mx, the Monod constant, Ks, and the maximum growth μmax were also fitted to the ODE equation set. We used information from experience and the available data to constrain the parameters.

89/2223/2 - Swithland Sand & Gravel (1972) Ltd. - Request for retention of building following completion of extraction and landfilling for use as an ...

Advanced Process Control (APC) is commonly defined as Model-based Process Control (MPC) plus Fault Detection and Classification (FDC) (Doering and Nishi 2007). Soft-sensors (also known as inferential models or virtual metrology) also fall under the APC umbrella. Figure 1 shows where MPC and Fault Detection and Classifi cation are in our proposed model maturity map (Romero-Torres, Wolfram et al. 2018). Soft sensors can help infer unmeasured, or unmeasurable, process variables. In addition, APC solutions can improve the controllability of complex processes which require multivariate controllers. In addition, a model-based predictive controller can be implemented to account for disturbances before they affect the process. As aforementioned in all these APC implementations, process models are needed. Process models with the intention of optimizing the process in real-time can be empirical, hybrid or mechanistic, see Figure 2.

The production of mAbs at large scale is typically done using a fedbatch configuration in which nutrients and glucose are fed into the broth based on estimated or measured demand. Since lactate is a product of the glucose metabolism, it will be affected by the fedbatch configuration and needs to be modeled as such. In this section the glucose-to-lactate relationship was modeled in addition to fedbatch mode associated volume changes (dV/dt) and dilution factors (Equation 2).

Subscribe to our e-Newsletters Stay up to date with the latest news, articles, and events. Plus, get special offers from American Pharmaceutical Review – all delivered right to your inbox! Sign up now!

Rearming Kit 0924. Contains: 1-33 gram cylinder with cylinder seal indicator; 1-Pill cage; Rearming instructions. Rearming kit for the following models only ...

Chris Antoniou has been a Distinguished Engineer at Biogen corporation for the last 13 years. He leads the Global Engineering Process Modeling Group focusing on process modeling and simulations, manufacturing analytics, development and implementation of new technologies and academia collaborations. Chris has more than 30 years of diversified experience in product and process development in cGMP manufacturing and is a Subject Matter Expert in both upstream and downstream processing. He has expertise in the design of small and large-scale manufacturing facilities including single use facilities for antibody production and gene therapy. Chris has a Bachelor’s and Master’s in Chemical Engineering from Manhattan College. He has a number of process and system design patents and numerous technical publications.

Empirical models require a significant amount of data, and depending on the process complexity, don’t off er the right level of robustness needed for process control. Mechanistic models are theoretically robust as they incorporate scientific principles but are difficult to make for complex systems. Hybrid models (combination of mechanistic and empirical) tend to offer a good compromise between modeling approaches. Hybrid modeling should offer more robustness than empirical models without needing equations to describe the impact of every possible degree of freedom (purely mechanistic). This is why for a complex system such as a bioreactor (see Figure 3), hybrid models can bring the robustness of mechanistic models and the flexibility of empirical approaches. Hybrid models can be included in a digital twin (also known as a virtual plant) (Figure 4) to continuously monitor and/or optimize the process performance. The next sections of this article will introduce a framework for a bioreactor model which can be further developed (augmented) into a model for MPC, training or for expedited development.

Figure 13 shows the results of the fitting process for an actual production bioreactor batch manufactured using a fed-bach configuration at manufacturing scale. For this model, the prediction for the cell density and lactate profiles closely matches the trends from the actual data. However, there is a mismatch between the simulated glucose profile and the actual glucose trajectory after day five. In order to address this complexity of the fed-batch setup, the glucose feedback loop was incorporated into the model. This will be discussed in the next section.

Technical Specification Item Swing Check Valve Material of Construction Cast Iron Size 3 Connection Type Flanged Length 9-1/2 Cap to Inlet Center 5-9/16 Max.

This review, we provide a critical summary of research efforts that emerged in the CADD community in response to the pandemic.

DMM GAME PLAYERはDMM GAMESのするPCソフトウェアですゲームやダウンロードオンラインゲームいりパッケージゲームのからプレイまでDMM GAME ...

Osmolality data was collected pre-feeding as well, nevertheless we included the effect of nutrient feeding on the osmolality for model accuracy. Osmolality on day three had an inflection point and gradually increased in the broth until the end of the bioreaction.

This approach of hybrid modeling with application to the cell growth, nutrients, metabolism, and process parameters utilized fundamental relationships, control strategies description and available data from a mAb process. The metabolism was modeled using a structured model capturing cell growth, glucose, glutamine, glutamate and ammonia. The glucose feedback loop was captured as well at the fed-batch process of nutrient feeding. All the parameters were optimized using a global search algorithm achieving greater than 80% agreement between the actual data and model prediction for most process conditions except ammonia and glutamine. Future work may require revising and/or augmenting the model for particular applications and molecules as well as incorporating the design system modeling space.

We would like to acknowledge Rohin Mhatre and the Biogen Technology Investment Committee for funding as well as Sarwat Khattak, Jun Ren, Suresh Nulu, Le Ly, Vinny Malikasim, and Biogen’s RTP Pilot Plant Team for their technical contributions and support.

For a simple simulator, we started with a basic model and added complexity based on available variables. These variables were obtained with online measurements (Raman, DO, pH, Temperature probes) and near line measurements (Blood Gas Analyzer and Absorption Spectrometer).

Dr. Syed Kaschif Ahmed has a Ph.D. in Chemical Engineering specializing in Advanced Process Control (APC) from the Illinois Institute of Technology. Kaschif has academic experience in modeling, optimizing, and controlling different systems such as fuel cell cars, coal gasifier, and hybrid electric cars. As a postdoctoral fellow for the Pacific Institute for Climate Solutions, he prepared a technoeconomic tool for City of Surrey and Simon Fraser University to evaluate alternative fueled vehicles. He gained industrial experience at Corning-NY where he designed Advanced Process Control solutions for new production lines in North America, Europe and Asia, while optimizing and improving existing lines. Kaschif is currently an APC engineer in the Advanced Data Analytics group in Biogen developing hybrid models and advanced controls for biologics’ upstream and downstream drug substance processes.

The simple titer model incorporated cell growth. Oxygen consumption was captured from the initial DO concentration. When the DO controller activates, the model used a PI controller to maintain DO. Osmolality and pH were modeled as simple piecewise lines. Piecewise modeling was conducted since there were different times of the bioreaction where these variables trended differently. These differences can be attributed to different process events. Some of these events are: initial adaptation to the basal media before day one and growth. After day three, the glucose feeding produces a pH drop until the process reaches the lag phase. When the process reaches the lag phase, there is a gradual pH increase.