∑ k = 0 ∞ sin ⁡ ( k x ) r k = 1 2 i [ ∑ k = 0 ∞ ( e i x r ) k − ∑ k = 0 ∞ ( e − i x r ) k ] . {\displaystyle \sum _{k=0}^{\infty }{\frac {\sin(kx)}{r^{k}}}={\frac {1}{2i}}\left[\sum _{k=0}^{\infty }\left({\frac {e^{ix}}{r}}\right)^{k}-\sum _{k=0}^{\infty }\left({\frac {e^{-ix}}{r}}\right)^{k}\right].}

is geometric because each successive term can be obtained by multiplying the previous term by 1 / 2 {\displaystyle 1/2} .

The geometric series a + a r + a r 2 + a r 3 + … {\displaystyle a+ar+ar^{2}+ar^{3}+\dots } has the same coefficient a {\displaystyle a} in every term.[9] The first term of a geometric series is equal to this coefficient and is the parameter a {\displaystyle a} of that geometric series, giving a {\displaystyle a} its common interpretation: the "initial term."

Let AA', BC, DD', EF be any multitude whatsoever of continuously proportional numbers, beginning from the least AA'. And let BG and FH, each equal to AA', have been subtracted from BC and EF. I say that as GC is to AA', so EH is to AA', BC, DD'.

a + a r + a r 2 + a r 3 + ⋯ + a r n = ∑ k = 0 n a r k . {\displaystyle a+ar+ar^{2}+ar^{3}+\dots +ar^{n}=\sum _{k=0}^{n}ar^{k}.}

Like the geometric series, a power series  a 0 + a 1 x + a 2 x 2 + … {\displaystyle a_{0}+a_{1}x+a_{2}x^{2}+\ldots }  has one parameter for a common variable raised to successive powers, denoted  x {\displaystyle x}  here, corresponding to the geometric series's r, but it has additional parameters  a 0 , a 1 , a 2 , … , {\displaystyle a_{0},a_{1},a_{2},\ldots ,} one for each term in the series, for the distinct coefficients of each  x 0 , x 1 , x 2 , … {\displaystyle x^{0},x^{1},x^{2},\ldots } , rather than just a single additional parameter  a {\displaystyle a}  for all terms, the common coefficient of  r k {\displaystyle r^{k}}  in each term of a geometric series.

Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line. Archimedes' theorem states that the total area under the parabola is 4/3 of the area of the blue triangle. His method was to dissect the area into an infinite number of triangles as shown in the adjacent figure.[2][3]

In mathematics, a geometric series is a series in which the ratio of successive adjacent terms is constant. In other words, the sum of consecutive terms of a geometric sequence forms a geometric series. Each term is therefore the geometric mean of its two neighbouring terms, similar to how the terms in an arithmetic series are the arithmetic means of their two neighbouring terms.

Euclid's Elements of Geometry "has the distinction of being the world's oldest continuously used mathematical textbook,"[20] and it includes a demonstration of the sum of finite geometric series in Book IX, Proposition 35, illustrated in an adjacent figure. The following is Euclid's terse proof of Proposition 35:[21]

Though geometric series are most commonly found and applied with the real or complex numbers for a {\displaystyle a} and r {\displaystyle r} , there are also important results and applications for matrix-valued geometric series, function-valued geometric series, p-adic number geometric series,[11] and, most generally, geometric series of elements of abstract algebraic fields, rings, and semirings.[12]

This initial term defines the units of measurement of the series as a whole, if it has any, and in applications it will often be named according to a noun with those units. For instance a {\displaystyle a} could be an "initial mass" in a radioactive decay problem, with units of mass of an isotope, an "initial payment" in mathematical finance, with units of some type of currency, or an "initial population" in demography or ecology, with units of a type such as nationality or species.

The area inside the Koch snowflake can be described as the union of infinitely many equilateral triangles (see figure). Each side of the green triangle is exactly 1/3 the size of a side of the large blue triangle, and therefore has exactly 1/9 the area. Similarly, each yellow triangle has 1/9 the area of a green triangle, and so forth. Taking the blue triangle as a unit of area, the total area of the snowflake is

The first term represents the area of the blue triangle, the second term the areas of the two green triangles, the third term the areas of the four yellow triangles, and so on. Simplifying the fractions gives

Using | S n − S | = | a r n + 1 1 − r | {\displaystyle |S_{n}-S|=\left|{\frac {ar^{n+1}}{1-r}}\right|} and setting q = 1 {\displaystyle q=1} gives

lim n → ∞ | S n + 1 − S | | S n − S | q = μ . {\displaystyle \lim _{n\rightarrow \infty }{\frac {\left|S_{n+1}-S\right|}{\left|S_{n}-S\right|^{q}}}=\mu .}

Archimedes determined that each green triangle has 1/8 the area of the blue triangle, each yellow triangle has 1/8 the area of a green triangle, and so forth. Assuming that the blue triangle has area 1, then, the total area is the sum of the infinite series

where r is the common ratio.[4][5] The case r = 1 {\displaystyle r=1} is just simple addition, a case of an arithmetic series. The formula for the partial sums S n {\displaystyle S_{n}} with r ≠ 1 {\displaystyle r\neq 1} can be derived as follows:[4][5][14][15] S n = a r 0 + a r 1 + ⋯ + a r n , r S n = a r 1 + a r 2 + ⋯ + a r n + 1 , S n − r S n = a r 0 − a r n + 1 , S n ( 1 − r ) = a ( 1 − r n + 1 ) , S n = a ( 1 − r n + 1 1 − r ) ,  for  r ≠ 1. {\displaystyle {\begin{aligned}S_{n}&=ar^{0}+ar^{1}+\cdots +ar^{n},\\rS_{n}&=ar^{1}+ar^{2}+\cdots +ar^{n+1},\\S_{n}-rS_{n}&=ar^{0}-ar^{n+1},\\S_{n}\left(1-r\right)&=a\left(1-r^{n+1}\right),\\S_{n}&=a\left({\frac {1-r^{n+1}}{1-r}}\right),{\text{ for }}r\neq 1.\end{aligned}}}

This convergence result is widely applied to prove the convergence of other series as well, whenever those series's terms can be bounded from above by a suitable geometric series; that proof strategy is the basis for the ratio test and root test for the convergence of infinite series.[4][5]

The first dimension is horizontal, in the bottom row, representing the geometric series with initial value a = 1 2 {\displaystyle a={\frac {1}{2}}} and common ratio r = 1 2 {\displaystyle r={\frac {1}{2}}}

This is the difference of two geometric series with initial terms equal to 1 and common ratios equal to e i x / r {\displaystyle e^{ix}/r} and e − i x / r {\displaystyle e^{-ix}/r} , and so the proof of the original proposition follows via two straightforward applications of the formula for infinite geometric series and then rearrangement of the result using e i x − e − i x 2 i = sin ⁡ ( x ) {\textstyle {\frac {e^{ix}-e^{-ix}}{2i}}=\sin(x)} and e i x + e − i x 2 = cos ⁡ ( x ) {\textstyle {\frac {e^{ix}+e^{-ix}}{2}}=\cos(x)} to complete the proof.

lim n → ∞ | a r n + 2 1 − r | | a r n + 1 1 − r | 1 = | r | = μ , {\displaystyle \lim _{n\rightarrow \infty }{\frac {\left|{\frac {ar^{n+2}}{1-r}}\right|}{\left|{\frac {ar^{n+1}}{1-r}}\right|^{1}}}=|r|=\mu ,}

∑ k = 0 ∞ a r 2 k + 1 = ∑ k = 0 ∞ ( a r ) ( r 2 ) k = a r 1 − r 2 . {\displaystyle \sum _{k=0}^{\infty }ar^{2k+1}=\sum _{k=0}^{\infty }(ar)(r^{2})^{k}={\frac {ar}{1-r^{2}}}.}

G s ( n , r ) = ∑ k = 0 s { s k } x k d k d x k [ 1 − x n + 1 1 − x ] {\displaystyle G_{s}(n,r)=\sum _{k=0}^{s}\left\lbrace {s \atop k}\right\rbrace x^{k}{\frac {d^{k}}{dx^{k}}}\left[{\frac {1-x^{n+1}}{1-x}}\right]}

In capital-sigma notation, ∑ k = 0 ∞ a r k , {\displaystyle \sum _{k=0}^{\infty }ar^{k},} this term is technically written a r 0 {\displaystyle ar^{0}} instead of the bare a {\displaystyle a} . This is equivalent because r 0 = 1 {\displaystyle r^{0}=1} for any number r . {\displaystyle r.}

Depending on context, convergence of order one is often called linear convergence, because the number of decimals of precision increase linearly with the number of terms n + 1 , {\displaystyle n+1,} or called exponential convergence, because the magnitude of the difference from the limit decreases exponentially with n . {\displaystyle n.} "Linear convergence" is especially common where the number of digits of accuracy is a natural focus of analysis, as in numerical analysis, and "exponential convergence" is especially common where absolute deviation is a natural focus of analysis, as in common cases in physics, economics, and biology.

∑ k = m ∞ a r k = ∑ k = 0 ∞ ( a r m ) r k = a r m 1 − r . {\displaystyle \sum _{k=m}^{\infty }ar^{k}=\sum _{k=0}^{\infty }(ar^{m})r^{k}={\frac {ar^{m}}{1-r}}.}

This formula is only strictly valid for | r | < 1 {\textstyle |r|<1} as well. From similar derivations, it follows that, for | r | < 1 : {\textstyle |r|<1:}

In cases where the sum does not start at k = 0, one can use a shift of the index of summation together with a variable substitution,

S n = { a ( n + 1 ) r = 1 a ( 1 − r n + 1 1 − r ) otherwise {\displaystyle {\begin{aligned}S_{n}={\begin{cases}a(n+1)&r=1\\a\left({\frac {1-r^{n+1}}{1-r}}\right)&{\text{otherwise}}\end{cases}}\end{aligned}}}

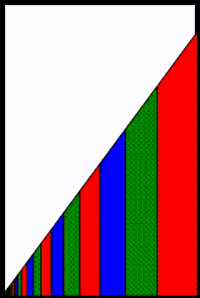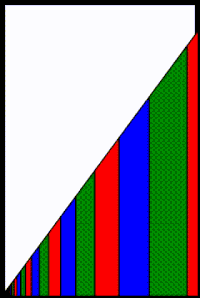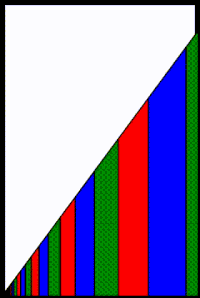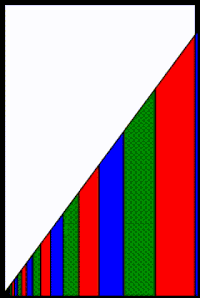
Alternatively, a geometric interpretation of the convergence for 0 < r < 1 {\displaystyle 0<1} is shown in the adjacent diagram. The area of the white triangle is the series remainder

within the range | r | < 1 {\displaystyle \vert r\vert <1} , with a = 1 / 2 {\displaystyle a=1/2} and r = 1 / 2 {\displaystyle r=1/2} in Oresme's particular example.

Although difficult to visualize beyond three dimensions, Oresme's insight in § Nicole Oresme (c.1323 – 1382) generalizes to any dimension d {\displaystyle d} . Denoting the sum of the d {\displaystyle d} -dimensional series S ( d ) {\displaystyle S(d)} , then using the limit of the ( d − 1 ) {\displaystyle (d-1)} -dimensional geometric series, S ( d − 1 ) , {\displaystyle S(d-1),} as the initial term of a geometric series with the same common ratio in the next dimension, results in a recursive formula for S ( d ) {\displaystyle S(d)} with the base case S ( 1 ) {\displaystyle S(1)} given by the usual sum formula with an initial term a {\displaystyle a} , so that:

The geometric series can therefore be considered a class of power series in which the sequence of coefficients satisfies  a k = a {\displaystyle a_{k}=a}  for all  k {\displaystyle k}  and  x = r {\displaystyle x=r} .[4][5] This special class of power series plays an important role in mathematics, for instance for the study of ordinary generating functions in combinatorics[7] and the summation of divergent series in analysis.[8] Many other power series can be written as transformations and combinations of geometric series, making the geometric series formula a convenient tool for calculating formulas for those power series as well.[7]

This sort of calculation is used to compute the APR of a loan (such as a mortgage loan). It can also be used to estimate the present value of expected stock dividends, or the terminal value of a financial asset assuming a stable growth rate. However, the assumption that interest rates are constant is generally incorrect and payments are unlikely to in fact continue forever since the issuer of the perpetual annuity may lose its ability or end its commitment to make continued payments, so estimates like these are only heuristic guidelines for decision making rather than scientific predictions of actual current values.

with initial term a = 1234 / 10000 {\displaystyle a=1234/10000} and common ratio r = 1 / 10000. {\displaystyle r=1/10000.} The geometric series formula provides an integer ratio that corresponds to the repeating decimal:

The partial sum of the first n + 1 {\displaystyle n+1} terms of a geometric series, up to and including the r n {\displaystyle r^{n}} term,

∑ k = 0 ∞ k r k = r ( 1 − r ) 2 ; ∑ k = 0 ∞ k 2 r k = r ( 1 + r ) ( 1 − r ) 3 ;  and  ∑ k = 0 ∞ k 3 r k = r ( 1 + 4 r + r 2 ) ( 1 − r ) 4 . {\displaystyle \sum _{k=0}^{\infty }kr^{k}={\frac {r}{\left(1-r\right)^{2}}};\sum _{k=0}^{\infty }k^{2}r^{k}={\frac {r\left(1+r\right)}{\left(1-r\right)^{3}}};{\text{ and }}\sum _{k=0}^{\infty }k^{3}r^{k}={\frac {r\left(1+4r+r^{2}\right)}{\left(1-r\right)^{4}}}.}

where t k {\displaystyle t_{k}} represents the k {\displaystyle k} -th-power term of the geometric series.

This approach extends beyond repeating decimals, that is, base ten, to repeating patterns in other bases such as binary, that is, base two. For example, the binary representation of the number 0.7777 … 10 {\displaystyle 0.7777\ldots _{10}} is 0.110001110001110001 … 2 {\displaystyle 0.110001110001110001\ldots _{2}} where the binary pattern 110001 repeats indefinitely. That binary representation can be written as a geometric series of binary terms,

In addition to his elegantly simple proof of the divergence of the harmonic series, Nicole Oresme[22] proved that the arithmetico-geometric series known as Gabriel's Staircase,[23]

Geometric series have been studied in mathematics from at least the time of Euclid in his work, Elements, which explored geometric proportions.[1] Archimedes further advanced the study through his work on infinite sums, particularly in calculating areas and volumes of geometric shapes (for instance calculating the area inside a parabola).[2][3] In the early development of modern calculus, they were paradigmatic examples of both convergent series and divergent series and thus came to be crucial references for investigations of convergence, for instance in the ratio test and root test for convergence[4][5] and in the definitions of rates of convergence.[6] Geometric series have further served as prototypes in the study of mathematical objects such as Taylor series,[4][5] generating functions,[7] and perturbation theories.[8]

The interpretation of k {\displaystyle k} as a time variable is often exactly correct in applications, such as the examples of amortized analysis of algorithmic complexity and calculating the present value of an annuity in § Applications below, where k {\displaystyle k} represents a count of years. In such applications it is also common to report a "growth rate" r {\displaystyle r} in terms of another expression such as ( r − 1 ) / 100 {\displaystyle (r-1)/100} , which is a percentage growth rate, or 1 / log 2 ⁡ r {\displaystyle 1/\log _{2}r} , which is a doubling time, the opposite of a half-life. These rate parameters must then have units of the inverse of the time units of k {\displaystyle k} , which may be years (then the rate is "per annum"), days (then the rate is "per diem"), or any other counts of regularly spaced events.

An example of how this behaves for θ {\displaystyle \theta } values that increase linearly over time with a constant angular frequency ω 0 {\displaystyle \omega _{0}} , such that θ = ω 0 t , {\displaystyle \theta =\omega _{0}t,} is shown in the adjacent video. For θ = ω 0 t , {\displaystyle \theta =\omega _{0}t,} the geometric series becomes

The terseness of Euclid's propositions and proofs may have been a necessity. The Elements of Geometry is over 500 pages of propositions and proofs in standard formats, and making copies of the textbook required making labor intensive manuscript copies for many centuries until the printing press was invented in 1440. Being terse reduced the work of making copies.

Truncated geometric series a + a r + a r 2 + a r 3 + ⋯ + a r n {\displaystyle a+ar+ar^{2}+ar^{3}+\dots +ar^{n}} are called "finite geometric series" in certain branches of mathematics, especially in 19th century calculus and in probability and statistics and their applications.

d d r ∑ k = 0 n r k = ∑ k = 1 n k r k − 1 = 1 − r n + 1 ( 1 − r ) 2 − ( n + 1 ) r n 1 − r . {\displaystyle {\frac {d}{dr}}\sum _{k=0}^{n}r^{k}=\sum _{k=1}^{n}kr^{k-1}={\frac {1-r^{n+1}}{(1-r)^{2}}}-{\frac {(n+1)r^{n}}{1-r}}.}

∑ k = 0 n a r 2 k + 1 = a r ( 1 − r 2 n + 2 ) 1 − r 2 {\displaystyle {\begin{aligned}\sum _{k=0}^{n}ar^{2k+1}&={\frac {ar(1-r^{2n+2})}{1-r^{2}}}\end{aligned}}}

For convenience, in this section, the sum of the geometric series will be denoted by S {\displaystyle S} and its partial sums (the sums of the series going up to only the nth power term) will be denoted S n . {\displaystyle S_{n}.}

An exact formula for any of the generalized sums G s ( n , r ) {\displaystyle G_{s}(n,r)} when s ∈ N {\displaystyle s\in \mathbb {N} } is

Most of the theorems appearing in the Elements were not discovered by Euclid himself, but were the work of earlier Greek mathematicians such as Pythagoras (and his school), Hippocrates of Chios, Theaetetus of Athens, and Eudoxus of Cnidos. However, Euclid is generally credited with arranging these theorems in a logical manner, so as to demonstrate (admittedly, not always with the rigour demanded by modern mathematics) that they necessarily follow from five simple axioms. Euclid is also credited with devising a number of particularly ingenious proofs of previously discovered theorems (e.g., Theorem 48 in Book I).

In applications with units of measurement, the initial term a {\displaystyle a} provides the units of the series and the common ratio r {\displaystyle r} is a dimensionless quantity.

T = S ( 1 + 1 2 + 1 4 + 1 8 + … ) = S 1 − r = 1 1 − 1 2 = 2. {\displaystyle {\begin{aligned}T&=S\left(1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\dots \right)\\&={\frac {S}{1-r}}={\frac {1}{1-{\frac {1}{2}}}}=2.\end{aligned}}}

Continuing with the simple model and assuming a constant interest rate, a payment of $100 two years in the future would have a present value of $ 100 / ( 1 + I ) 2 {\displaystyle \$100/(1+I)^{2}} (squared because two years' worth of interest is lost by not receiving the money right now). Continuing that line of reasoning, the present value of receiving $100 per year in perpetuity would be

As a power series, the geometric series has a radius of convergence of 1.[4][5] This could be seen as a consequence of the Cauchy–Hadamard theorem and the fact that lim n → ∞ a n = 1 {\textstyle \lim _{n\rightarrow \infty }{\sqrt[{n}]{a}}=1} for any a {\displaystyle a} or as a consequence of the ratio test for the convergence of infinite series, with lim n → ∞ | a r n + 1 | / | a r n | = | r | {\textstyle \lim _{n\rightarrow \infty }|ar^{n+1}|/|ar^{n}|=|r|} implying convergence only for | r | < 1. {\displaystyle |r|<1.} However, both the ratio test and the Cauchy–Hadamard theorem are proven using the geometric series formula as a logically prior result, so such reasoning would be subtly circular.[4][5]

so the order of convergence of the geometric series is 1, its rate of convergence is | r | {\displaystyle |r|} , and the number of extra decimals of precision per term in the approach to the limit is − log 10 ⁡ r . {\displaystyle -\log _{10}r.} [17]

In order to analyze the convergence of these general geometric series, then on top of addition and multiplication, one must also have some metric of distance between partial sums of the series. This can introduce new subtleties into the questions of convergence, such as the distinctions between uniform convergence and pointwise convergence in series of functions, and can lead to strong contrasts with intuitions from the real numbers, such as in the convergence of the series 1 + 2 + 4 + 8 + ... with a = 1 {\displaystyle a=1} and r = 2 {\displaystyle r=2} to a / ( 1 − r ) = − 1 {\textstyle a/(1-r)=-1} in the 2-adic numbers using the 2-adic absolute value as a convergence metric. In that case the 2-adic absolute value of the common coefficient is | r | 2 = | 2 | 2 = 1 / 2 {\displaystyle |r|_{2}=|2|_{2}=1/2} , and while this is counterintuitive from the perspective of real number absolute value (where | 2 | = 2 , {\displaystyle |2|=2,} naturally), it is nonetheless well-justified in the context of p-adic analysis.[11]

∑ k = 0 ∞ a r 2 k = ∑ k = 0 ∞ a ( r 2 ) k = a 1 − r 2 {\displaystyle \sum _{k=0}^{\infty }ar^{2k}=\sum _{k=0}^{\infty }a(r^{2})^{k}={\frac {a}{1-r^{2}}}}

∑ k = 1 ∞ k r k − 1 = d d r ∑ k = 0 ∞ r k = 1 ( 1 − r ) 2 . {\displaystyle \sum _{k=1}^{\infty }kr^{k-1}={\frac {d}{dr}}\sum _{k=0}^{\infty }r^{k}={\frac {1}{(1-r)^{2}}}.}

In contrast, with r > 1 {\displaystyle r>1} the sequences of triangles and of trapezoids representing the terms of the series would instead get progressively wider and taller and farther from the origin, not converging to the origin as terms and also not converging in sum as a series.

An example that has four digits is the repeating decimal pattern, 0.123412341234.... {\displaystyle 0.123412341234....} This can be written as the geometric series

When the series converges, the rate of convergence gets slower as | r | {\displaystyle |r|} approaches 1 {\displaystyle 1} ; see § Rate of convergence.[4][5][6] The pattern of convergence also depends on the sign or complex argument of the common ratio. If r > 0 {\displaystyle r>0} and | r | < 1 {\displaystyle |r|<1} then terms all share the same sign and the partial sums of the terms approach their eventual limit monotonically. If r < 0 {\displaystyle r<0} and | r | < 1 {\displaystyle |r|<1} , adjacent terms in the geometric series alternate between positive and negative and the partial sums S n {\displaystyle S_{n}} of the terms oscillate above and below their eventual limit S {\displaystyle S} . For complex r {\displaystyle r} and | r | < 1 , {\displaystyle |r|<1,} the S n {\displaystyle S_{n}} converge in a spiraling pattern.

∑ k = 0 ∞ sin ⁡ ( k x ) r k = r sin ⁡ ( x ) 1 + r 2 − 2 r cos ⁡ ( x ) . {\displaystyle \sum _{k=0}^{\infty }{\frac {\sin(kx)}{r^{k}}}={\frac {r\sin(x)}{1+r^{2}-2r\cos(x)}}.}

This approach generalizes usefully to higher dimensions, and that generalization is described below in § Connections to power series.

As n {\displaystyle n} approaches infinity, the absolute value of r must be less than one for this sequence of partial sums to converge to a limit. When it does, the series converges absolutely.[4][5] The infinite series then becomes S = a + a r + a r 2 + a r 3 + a r 4 + ⋯ = lim n → ∞ S n = lim n → ∞ a ( 1 − r n + 1 ) 1 − r = a 1 − r − a 1 − r lim n → ∞ r n + 1 = a 1 − r  for  | r | < 1. {\displaystyle {\begin{aligned}S&=a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots \\&=\lim _{n\rightarrow \infty }S_{n}\\&=\lim _{n\rightarrow \infty }{\frac {a(1-r^{n+1})}{1-r}}\\&={\frac {a}{1-r}}-{\frac {a}{1-r}}\lim _{n\rightarrow \infty }r^{n+1}\\&={\frac {a}{1-r}}{\text{ for }}|r|<1.\end{aligned}}}

The geometric series a + a r + a r 2 + a r 3 + … {\displaystyle a+ar+ar^{2}+ar^{3}+\dots } is an infinite series derived from a special type of sequence called a geometric progression, which is defined by just two parameters: the initial term a {\displaystyle a} and the common ratio r {\displaystyle r} . Finite geometric series a + a r + a r 2 + a r 3 + ⋯ + a r n {\displaystyle a+ar+ar^{2}+ar^{3}+\dots +ar^{n}} have a third parameter, the final term's power n . {\displaystyle n.}

When r > 1 {\displaystyle r>1} it is often called a growth rate or rate of expansion and when 0 < r < 1 {\displaystyle 0<1} it is often called a decay rate or shrink rate, where the idea that it is a "rate" comes from interpreting k {\displaystyle k} as a sort of discrete time variable. When an application area has specialized vocabulary for specific types of growth, expansion, shrinkage, and decay, that vocabulary will also often be used to name r {\displaystyle r} parameters of geometric series. In economics, for instance, rates of increase and decrease of price levels are called inflation rates and deflation rates, while rates of increase in values of investments include rates of return and interest rates.

For any sequence x n {\displaystyle x_{n}} , its rate of convergence to a limit value x L {\displaystyle x_{L}} is determined by the parameters q {\displaystyle q} and μ {\displaystyle \mu } such that

Decimal numbers that have repeated patterns that continue forever, for instance 0.7777 … , {\displaystyle 0.7777\ldots ,} 0.9999 … , {\displaystyle 0.9999\ldots ,} or 0.123412341234 … , {\displaystyle 0.123412341234\ldots ,} can be interpreted as geometric series and thereby converted to expressions of the ratio of two integers.[24] For example, the repeated decimal fraction 0.7777 … {\displaystyle 0.7777\ldots } can be written as the geometric series

In contrast, a general power series a 0 + a 1 r + a 2 r 2 + a 3 r 3 + … {\displaystyle a_{0}+a_{1}r+a_{2}r^{2}+a_{3}r^{3}+\dots } would have coefficients a k {\displaystyle a_{k}} that could vary from term to term. In other words, the geometric series is a special case of the power series. Connections between power series and geometric series are discussed below in the section § Connections to power series.

The common ratio r {\displaystyle r} can also be a complex number given by | r | e i θ {\displaystyle \vert r\vert e^{i\theta }} , where | r | {\displaystyle |r|} is the magnitude of the number as a vector in the complex plane, θ {\displaystyle \theta } is the angle or argument of that vector, e {\displaystyle e} is Euler's number, and i 2 = − 1 {\displaystyle i^{2}=-1} . In this case, the expanded form of the geometric series is

In general, a geometric series is written as a + a r + a r 2 + a r 3 + . . . {\displaystyle a+ar+ar^{2}+ar^{3}+...} , where a {\displaystyle a} is the initial term and r {\displaystyle r} is the common ratio between adjacent terms.[4][5] For example, the series

Any finite geometric series has the sum a ( 1 − r n + 1 ) / ( 1 − r ) {\displaystyle a(1-r^{n+1})/(1-r)} , and when | r | < 1 {\displaystyle |r|<1} the infinite series converges to the limit value a / ( 1 − r ) {\displaystyle a/(1-r)} .

The second dimension is vertical, where the bottom row is a new initial term a = S {\displaystyle a=S} and each subsequent row above it shrinks according to the same common ratio r = 1 2 {\displaystyle r={\frac {1}{2}}} , making another geometric series with sum T {\displaystyle T} ,

The first term of this series represents the area of the blue triangle, the second term the total area of the three green triangles, the third term the total area of the twelve yellow triangles, and so forth. Excluding the initial 1, this series is geometric with constant ratio r = 4/9. The first term of the geometric series is a = 3(1/9) = 1/3, so the sum is

where the initial term is a = 110001 2 / 1000000 2 {\displaystyle a=110001_{2}/1000000_{2}} expressed in base two = 49 10 / 64 10 {\displaystyle =49_{10}/64_{10}} in base ten and the common ratio is r = 1 / 1000000 2 {\displaystyle r=1/1000000_{2}} in base two = 1 / 64 10 {\displaystyle =1/64_{10}} in base ten. Using the geometric series formula as before,

One can use simple variable substitutions to calculate some useful closed form infinite series formulas. For an infinite series containing only even powers of r {\displaystyle r} , for instance,

For example, suppose that a payment of $100 will be made to the owner of the perpetual annuity once per year at the end of the year. In one simple model of the present value of future money, receiving $100 a year from now is worth less than an immediate $100 if one could invest the money now at a favorable interest rate. In particular, in that case, given a positive yearly interest rate I {\displaystyle I} , the cost of an investment that produces $100 in the future is just $ 100 / ( 1 + I ) {\textstyle \$100/(1+I)} today, so the present value of $100 one year in the future is $ 100 / ( 1 + I ) {\textstyle \$100/(1+I)} today. More complex models of present value might account for the relative purchasing power of money today and in the future or account for changing personal utilities for having money now and in the future.

The parameter r {\displaystyle r} is called the common ratio because it is the ratio of any term with the previous term in the series.

The convergence of the infinite sequence of partial sums of the infinite geometric series depends on the magnitude of the common ratio r {\displaystyle r} alone:

The formula holds for real number r {\displaystyle r} and for complex number r {\displaystyle r} , and it can also be generalized to matrix r {\displaystyle r} or p-adic number r {\displaystyle r} , but for the latter generalizations and technical conditions for their convergence see § Generalizations beyond real and complex values.

The Taylor series expansion of the arctangent function around zero, called the arctangent series, has been an important means for making approximate calculations in astronomy and optics for hundreds of years. It is traditionally called Gregory's series in Europe after the Scottish astronomer and mathematician James Gregory (1638 – 1675) though it is today more commonly attributed to the Keralan astronomer and mathematician Madhava of Sangamagrama (c. 1340 – c. 1425). It can be derived using differentiation, integration, and the sum of a geometric series.

where the initial term is a = 7 / 10 {\displaystyle a=7/10} and the common ratio is r = 1 / 10 {\displaystyle r=1/10} . The geometric series formula provides the integer ratio that corresponds to the repeating decimal:

2,500 years ago, Greek mathematicians believed[19] that an infinitely long list of positive numbers must sum to infinity. Therefore, Zeno of Elea created a paradox when he demonstrated that in order to walk from one place to another, one must first walk half the distance there, and then half of the remaining distance, and half of that remaining distance, and so on, covering infinitely many intervals before arriving. In doing so, he partitioned a fixed distance into an infinitely long list of halved remaining distances, each of which has length greater than zero. Zeno's paradox revealed to the Greeks that their assumption about an infinitely long list of positive numbers needing to add up to infinity was incorrect.

Therefore, letting the arctan function equal the integral arctan ⁡ ( x ) = ∫ d x 1 + x 2 in the range  − π / 2 < arctan ⁡ ( x ) < π / 2 , = ∫ d x 1 − ( − x 2 ) by writing integrand as closed form of geometric series with  r = − x 2 , = ∫ ( 1 + ( − x 2 ) + ( − x 2 ) 2 + ( − x 2 ) 3 + ⋯ ) d x by writing geometric series in expanded form , = ∫ ( 1 − x 2 + x 4 − x 6 + ⋯ ) d x by calculating the sign and power of each term in integrand , = x − x 3 3 + x 5 5 − x 7 7 + ⋯ by integrating each term , = ∑ n = 0 ∞ ( − 1 ) n 2 n + 1 x 2 n + 1 by writing series in generator form . {\displaystyle {\begin{aligned}\arctan(x)&=\int {\frac {dx}{1+x^{2}}}\quad &&{\text{in the range }}-\pi /2<\arctan(x)<\pi /2,\\&=\int {\frac {dx}{1-(-x^{2})}}\quad &&{\text{by writing integrand as closed form of geometric series with }}r=-x^{2},\\&=\int \left(1+\left(-x^{2}\right)+\left(-x^{2}\right)^{2}+\left(-x^{2}\right)^{3}+\cdots \right)dx\quad &&{\text{by writing geometric series in expanded form}},\\&=\int \left(1-x^{2}+x^{4}-x^{6}+\cdots \right)dx\quad &&{\text{by calculating the sign and power of each term in integrand}},\\&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \quad &&{\text{by integrating each term}},\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}\quad &&{\text{by writing series in generator form}}.\end{aligned}}} This is the power series expansion of the arctangent function.

Geometric series have been applied to model a wide variety of natural phenomena and social phenomena, such as the expansion of the universe where the common ratio between terms is defined by Hubble's constant, the decay of radioactive carbon-14 atoms where the common ratio between terms is defined by the half-life of carbon-14, probabilities of winning in games of chance where the common ratio could be determined by the odds of a roulette wheel, and the economic values of investments where the common ratio could be determined by a combination of inflation rates and interest rates.

When the multiplication of the parameters is not commutative, as it often is not for matrices or general physical operators, particularly in quantum mechanics, then the standard way of writing the geometric series, a + a r + a r 2 + a r 3 + . . . {\displaystyle a+ar+ar^{2}+ar^{3}+...} , multiplying from the right, may need to be distinguished from the alternative a + r a + r 2 a + r 3 a + . . . {\displaystyle a+ra+r^{2}a+r^{3}a+...} , multiplying from the left, and also the symmetric a + r 1 / 2 a r 1 / 2 + r a r + r 3 / 2 a r 3 / 2 + . . . {\displaystyle a+r^{1/2}ar^{1/2}+rar+r^{3/2}ar^{3/2}+...} , multiplying half on each side. These choices may correspond to important alternatives with different strengths and weaknesses in applications, as in the case of ordering the mutual interferences of drift and diffusion differently at infinitesimal temporal scales in Ito integration and Stratonovitch integration in stochastic calculus.

For example, if the yearly interest rate is 10% ( I = 0.10 ) , {\textstyle (I=0.10),} then the entire annuity has an estimated present value of $ 100 / 0.10 = $ 1000. {\textstyle \$100/0.10=\$1000.}

where { s k } {\displaystyle \left\lbrace {s \atop k}\right\rbrace } denotes a Stirling number of the second kind.[26][27]

It is also possible to use complex geometric series to calculate the sums of some trigonometric series using complex exponentials and Euler's formula. For example, consider the proposition

The common ratio r {\displaystyle r} can be thought of as a multiplier used to calculate each next term in the series from the previous term. It must be a dimensionless quantity.

To eliminate these gaps, broaden each trapezoid so that it spans the rightmost 1 − r 2 {\displaystyle 1-r^{2}} of the original triangle area instead of just the rightmost 1 − | r | = 1 + r . {\displaystyle 1-|r|=1+r.} At the same time, to ensure the areas of the trapezoids remain consistent during this transformation, a rescaling is necessary. The required scaling factor λ {\displaystyle \lambda } can be derived from the equation:

While geometric series with real and complex number parameters a {\displaystyle a} and r {\displaystyle r} are most common, geometric series of more general terms such as functions, matrices, and p-adic numbers[11] also find application. The mathematical operations used to express a geometric series given its parameters are simply addition and repeated multiplication, and so it is natural, in the context of modern algebra, to define geometric series with parameters from any ring or field.[28] Further generalization to geometric series with parameters from semirings is more unusual, but also has applications, for instance in the study of fixed-point iteration of transformation functions.

In economics, specifically in mathematical finance, geometric series are used to represent the present values of perpetual annuities (sums of money to be paid each year indefinitely into the future).

The next adjacent diagram provides a geometric interpretation of a converging alternating geometric series with − 1 < r ≤ 0 , {\displaystyle -1

In the case of the sequence of partial sums of the geometric series, the relevant sequence is S n {\displaystyle S_{n}} and its limit is S {\displaystyle S} . Therefore, the rate and order are found via

S = 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + ⋯ = 1 2 1 − 1 2 = 1 {\displaystyle {\begin{aligned}S&={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+{\frac {1}{32}}+\dots ={\frac {\frac {1}{2}}{1-{\frac {1}{2}}}}=1\end{aligned}}}

Each additional term in the partial series reduces the area of that white triangle remainder by the area of the trapezoid representing the added term. The trapezoid shapes get progressively thinner and shorter and closer to the origin, corresponding to the trapezoid areas (i.e., the values of the terms) becoming smaller. As the number of trapezoids approaches infinity, the white triangle remainder will vanish and therefore S n {\displaystyle S_{n}} will converge to S {\displaystyle S} .

The derivative of f ( x ) = arctan ⁡ ( u ( x ) ) {\displaystyle f(x)=\arctan(u(x))} is known to be f ′ ( x ) = u ′ ( x ) ( 1 + [ u ( x ) ] 2 ) {\displaystyle f'(x)={\frac {u'(x)}{(1+[u(x)]^{2})}}} . This is a standard result derived as follows. Let y {\displaystyle y} and u {\displaystyle u} represent f ( x ) {\displaystyle f(x)} and u ( x ) {\displaystyle u(x)} ,[25]

As r {\displaystyle r} approaches 1, polynomial division or L'Hospital's rule recovers the case S n = a ( n + 1 ) {\displaystyle S_{n}=a(n+1)} .[16]

q {\displaystyle q} is called the order of convergence, while μ {\displaystyle \mu } is called the rate of convergence, where smaller μ {\displaystyle \mu } corresponds to faster convergence: when q = 1 {\displaystyle q=1} the asymptotic number of further decimals of precision of agreement with the limiting value per term of the series is − log 10 ⁡ μ ; {\displaystyle -\log _{10}\mu ;} the examples of μ = 1 / 10 {\displaystyle \mu =1/10} and μ = 1 / 100 {\displaystyle \mu =1/100} are especially simple to use to confirm that formula and intuition.

For a series with only odd powers of ⁠ r {\displaystyle r} ⁠, take a r {\displaystyle ar} for a {\displaystyle a} and r 2 {\displaystyle r^{2}} for r {\displaystyle r} in the standard form:

Like for the infinite series, one can use variable substitutions and changes of the index of summation to derive other finite power series formulas from the finite geometric series formulas. If one were to begin the sum not from k = 0 {\displaystyle k=0} but from a different value, say ⁠ m {\displaystyle m} ⁠, then ∑ k = m n a r k = { a ( r m − r n + 1 ) 1 − r if  r ≠ 1 a ( n − m + 1 ) if  r = 1 {\displaystyle {\begin{aligned}\sum _{k=m}^{n}ar^{k}&={\begin{cases}{\frac {a(r^{m}-r^{n+1})}{1-r}}&{\text{if }}r\neq 1\\a(n-m+1)&{\text{if }}r=1\end{cases}}\end{aligned}}} For a geometric series containing only even powers of r {\displaystyle r} , take r 2 {\displaystyle r^{2}} as the common ratio r {\displaystyle r} and use the standard formula to find ∑ k = 0 n a r 2 k = a ( 1 − r 2 n + 2 ) 1 − r 2 {\displaystyle {\begin{aligned}\sum _{k=0}^{n}ar^{2k}&={\frac {a(1-r^{2n+2})}{1-r^{2}}}\end{aligned}}}

where − 1 < r ≤ 0. {\displaystyle -1

To help translate the proposition and proof into a form that uses current notation, a handful of modifications are present in the adjacent figure. First, the four horizontal line lengths representing the values of the first four terms of a geometric series are now labeled a, ar, ar2, ar3 in the diagram's left margin. Second, new labels A' and D' are now on the first and third lines so that all the diagram's line segment names consistently specify the segment's starting point and ending point.

This is a geometric series with common ratio 1 / ( 1 + I ) . {\displaystyle 1/(1+I).} The sum is the first term divided by (one minus the common ratio):

where the first term is a vector of length a {\displaystyle a} that does not change orientation and all the following terms are vectors of proportional lengths rotating in the complex plane at integer multiples of the fundamental angular frequency ω 0 {\displaystyle \omega _{0}} , also known as harmonics of ω 0 {\displaystyle \omega _{0}} . As the video shows, these sums trace a circle. The period of rotation around the circle is 2 π / ω 0 {\displaystyle 2\pi /\omega _{0}} .

S n = a r 0 + a r 1 + ⋯ + a r n = ∑ k = 0 n a r k , {\displaystyle {\begin{aligned}S_{n}&=ar^{0}+ar^{1}+\cdots +ar^{n}\\&=\sum _{k=0}^{n}ar^{k},\end{aligned}}}

For let FK be made equal to BC, and FL to DD'. And since FK is equal to BC, of which FH is equal to BG, the remainder HK is thus equal to the remainder GC. And since as EF is to DD', so DD' to BC, and BC to AA' [Prop. 7.13], and DD' equal to FL, and BC to FK, and AA' to FH, thus as EF is to FL, so LF to FK, and FK to FH. By separation, as EL to LF, so LK to FK, and KH to FH [Props. 7.11, 7.13]. And thus as one of the leading is to one of the following, so (the sum of) all of the leading to (the sum of) all of the following [Prop. 7.12]. Thus, as KH is to FH, so EL, LK, KH to LF, FK, HF. And KH equal to CG, and FH to AA', and LF, FK, HF to DD', BC, AA'. Thus, as CG is to AA', so EH to DD', BC, AA'. Thus, as the excess of the second is to the first, so is the excess of the last is to all those before it. The very thing it was required to show.

After the gaps are removed, pairs of terms in the converging alternating geometric series form a new converging geometric series with a common ratio r 2 , {\displaystyle r^{2},} reflecting the pairing of terms. The rescaled coefficient a = 1 / ( 1 − r ) {\displaystyle a=1/(1-r)} compensates for the gap-filling.

This computation is an example of the method of exhaustion, an early version of integration. Using calculus, the same area could be found by a definite integral.

lim n → ∞ | x n + 1 − x L | | x n − x L | q = μ . {\displaystyle \lim _{n\rightarrow \infty }{\frac {\left|x_{n+1}-x_{L}\right|}{\left|x_{n}-x_{L}\right|^{q}}}=\mu .} [17]